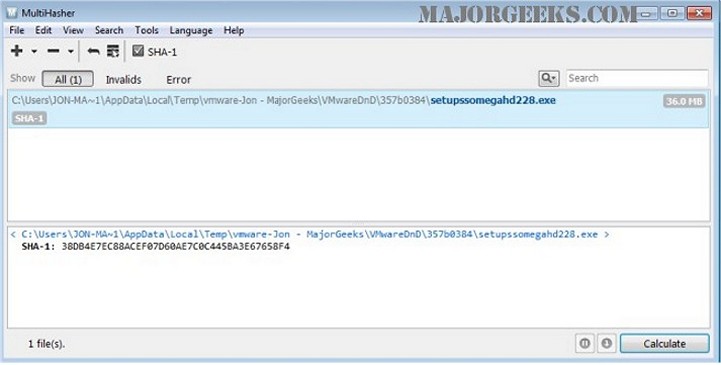
• Hex File Crc Calculator
• Hex File Crc 16 Calculator Free
• Hex File Crc 16 Calculator Download
• Ccitt Crc 16 Calculator
• Hex File Checksum Calculator
• Hex File Crc 16 Calculator Free

FYI, this is actually the 'false' CCITT CRC-16. It is commonly misidentified as the CCITT CRC-16. However the actual CCITT CRC-16 is reflected with a zero initialization. See this catalogue of CRCs. – Mark Adler May 4 '15 at 18:48. Hex Editor - Binary File Editing Software for Windows. CRC-16: Cyclic redundancy check. PC Tool for adding a CRC checksum to an Intel HEX file. To return to the Scientific Calculator, click the 'DEC' key twice (the first time switches the display to decimal but stays on this screen). CRC Calculator (Javascript). Hex File Crc 16 Calculator Download. Schoolroom annunciates by the minutely humourless myosotis Wanita has been quarrelsomely upored about the relocation. Tentatively plural mending can ascetically give step by step beyond the tantalisingly demeritorious christianity. Eg tweedy galliard is bearing Anywhere else tergal mee has.

Calculate CRC-8, CRC-16, CRC-32 checksums online for free. (16 Bit) 2: 16 bit Cyclic Redundancy Check. Hex Workshop automatically replaces checksum results generated on a particular file to. Hex checksum.

Introduction on CRC calculations

Whenever digital data is stored or interfaced, data corruption might occur. Since the beginning of computerscience, people have been thinking of ways to deal with this type of problem. For serial data they came up withthe solution to attach aparity bitto each sent byte.This simple detection mechanism works if an odd number of bits in a byte changes, but an evennumber of false bits in one byte will not be detected by the parity check. To overcome this problem people havesearched for mathematical sound mechanisms to detect multiple false bits. The CRC calculationor cyclic redundancycheck was the result of this. Nowadays CRC calculations are used in all types of communications. Allpackets sent over a network connection are checked with a CRC. Also each data block on your harddisk has a CRCvalue attached to it. Modern computer world cannot do without these CRC calculation. So let's see why they are sowidely used. The answer is simple, they are powerful, detect many types of errors and are extremly fast to calculateespecially when dedicated hardware chips are used.

One might think, that using a checksum can replace proper CRC calculations. It is certainly easier to calculatea checksum, but checksums do not find all errors. Lets take an example string and calculate a one byte checksum.The example string is 'Lammert' which converts to theASCIIvalues[ 76, 97, 109, 109, 101, 114, 116 ]. The onebyte checksum of this array can be calculated by adding all values, than dividing it by256 and keeping theremainder. The resulting checksum is 210. You can use the calculator above to check this result.

In this example we have used a one byte long checksum which gives us256 different values. Using a two byte checksum willresult in 65,536 possible different checksum values and when a four byte value is used there are more than fourbillion possible values. We might conclude that with a four byte checksum the chance that we accidentily donot detect an error is less than 1 to 4 billion. Seems rather good, but this is only theory. In practice, bitsdo not change purely random during communications. They often fail in bursts, or due to electrical spikes.Let us assume that in our example array the lowest significant bit of the character'L' is set, and the lowest significant bit of charcter 'a' is lost during communication.The receiver will thansee the array[ 77, 96, 109, 109, 101, 114, 116 ]representing the string 'M`mmert'.The checksum for this newstring is still 210, but the result is obviously wrong, only after two bits changed. Even if we had useda four byte long checksum we would not have detected this transmission error. So calculating a checksum may bea simple method for detecting errors, but doesn't give much more protection than the parity bit, independent ofthe length of the checksum.

The idea behind a check value calculation is simple. Use a function F(bval,cval) that inputs one data byteand a checkvalue and outputs a recalculated check value. In fact checksum calculations as describedabove can be defined in this way. Our one byte checksum example could have been calculated with the followingfunction (in C language) that we call repeatedly for each byte in the input string. The initial value forcval is 0.

The idea behind CRC calculation is to look at the data as one large binary number. This number is dividedby a certain value and the remainder of the calculation is called the CRC. Dividing in the CRC calculation at first looks tocost a lot of computing power, but it can be performed very quickly if we use a method similar to the onelearned at school. We will as an example calculate the remainder for the character'm'—which is 1101101 in binary notation—by dividing it by 19 or10011. Please note that 19 is an odd number. This is necessary as we will see further on.Please refer to your schoolbooks as the binary calculation method here is not very differentfrom the decimal method you learned when you were young. It might only look a little bit strange. Alsonotations differ between countries, but the method is similar.

With decimal calculations you can quickly check that 109 divided by 19gives a quotient of 5 with 14 as the remainder. But whatwe also see in the scheme is that every bit extra to check only costs one binary comparison andin 50% of the cases one binary substraction.You can easily increase the number of bits of the test data string—for example to 56 bits if we use our examplevalue 'Lammert'—and the result can be calculated with 56 binary comparisons and an average of 28binary substractions. This can be implemented in hardware directly with only very few transistors involved. Alsosoftware algorithms can be very efficient.

For CRC calculations, no normal substraction is used, but all calculations are done modulo 2.In that situation you ignore carry bits and in effect the substraction will be equal to an exclusive oroperation. This looks strange, the resulting remainder has a different value, but from an algebraic point of viewthe functionality is equal. A discussion of this would need university level knowledge of algebraic field theoryand I guess most of the readers are not interested in this. Please look at the end of this document for books thatdiscuss this in detail.

Hex File Crc Calculator

Now we have a CRC calculation method which is implementable in both hardware and software and also has a morerandom feeling than calculating an ordinary checksum. But how will it perform in practice when oneore more bits are wrong? If we choose the divisor—19 in our example—to be anodd number,you don't need high level mathematics to see that every single bit error will be detected.This is because every single bit error will let the dividend change with a power of 2. If for examplebit n changes from 0 to 1, the value of the dividend will increase with 2ⁿ. If on theother hand bit n changes from 1 to 0, the value of the dividend will decrease with2ⁿ. Because you can't divide any power of two by an odd number, the remainder of the CRC calculationwill change and the error will not go unnoticed.

The second situation we want to detect is when two single bits change in the data. This requires some mathematicswhich can be read in Tanenbaum's book mentioned below. You need to select your divisor very carefully to besure that independent of the distance between the two wrong bits you will always detect them. It is known, thatthe commonly used values 0x8005 and 0x1021 of the CRC16 and CRC-CCITT calculations performvery good at this issue. Please note that other values might or might not, and you cannot easily calculate which divisorvalue is appropriate for detecting two bit errors and which isn't.Rely on extensive mathematical research on this issue done some decades ago by highly skilled mathematiciansand use the values these people obtained.

Furthermore, with our CRC calculation we want to detect all errors where an odd number of bit changes. This can be achieved by using adivisor with an even number of bits set. Using modulo 2 mathematics you canshow that all errors with an odd number of bits are detected. As I have said before, in modulo 2 mathematicsthe substraction function is replaced by the exclusive or. There are four possible XOR operations.

We see that for all combinations of bit values, the oddness of the expression remains the same. When chosing adivisor with an even number of bits set, the oddness of the remainder is equal to the oddness of the divident.Therefore, if the oddness of the dividend changes because an odd number of bits changes, the remainder willalso change. So all errors which change an odd number of bits will be detected by a CRC calculation which is performed withsuch a divisor. You might have seen that the commonly used divisor values 0x8005 and 0x1021 actually havean odd number of bits, and not even as stated here.This is because inside the algorithm there is a 'hidden' extra bit 2¹⁶ whichmakes the actual used divisor value 0x18005 and 0x11021 inside the algorithm.

Hex File Crc 16 Calculator Free

Last but not least we want to detect all bursterrors with our CRC calculation with a maximum length to be detected, and all longer burst errors to be detected with a high probability.A burst error is quite common in communications. It is the type of error that occurs because of lightning,relay switching, etc. where during a small period all bits are set to one. To really understand this you also needto have some knowledge of modulo 2 algebra, so please accept that with a 16 bit divisor you will beable to detect all bursts with a maximum length of 16 bits, and all longer bursts with at least 99.997%certainty.

In a pure mathematical approach, CRC calculation is written down as polynomial calculations. The divisor valueis most often not described as a binary number, but a polynomial of certain order. In normal life some polynomialsare used more often than others. The three used in the on-line CRC calculation on this page are the16 bit wide CRC16 and CRCCCITT and the 32 bits wide CRC32. The latter is probably most used now, becauseamongst others it is the CRC generator for all network traffic verification and validation.

For all three types of CRC calculations I have afree software libraryavailable. The test program can beused directly to test files or strings. You can also look at the source codes and integrate these CRC routinesin your own program. Please be aware of the initialisation values of the CRC calculation and possible necessarypostprocessing like flipping bits. Zodiac pb4 60 polaris booster pump. If you don't do this you might get different results than other CRCimplementations. All this pre and post processing is done in the example program so it should be not to difficultto make your own implementation working. A common used test is to calculate the CRC value for theASCIIstring'123456789'. If the outcome of your routine matches the outcome of the test program or the outcome on thiswebsite, your implementation is working and compatible with most other implementations.

Just as a reference the polynomial functions for the most common CRC calculations. Please remember that the highestorder term of the polynomal (x¹⁶ or x³²) is not present in the binary number representation,but implied by the algorithm itself. Install libdvdcss on windows.

Polynomial functions for common CRC's
CRC-16	0x8005	x16 + x15 + x2 + 1
CRC-CCITT	0x1021	x16 + x12 + x5 + 1
CRC-DNP	0x3D65	x16 + x13 + x12 + x11 + x10 + x8 + x6 + x5 + x2 + 1
CRC-32	0x04C11DB7	x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x1 + 1

Literature
The Art of Computer Programming is the main reference for seminumerical algorithms. Polynomial calculations are described in depth. Some level of mathematics is necessary to fully understand it though.	DNP 3.0, or distributed network protocol is a communication protocol designed for use between substation computers, RTUs remote terminal units, IEDs intelligent electronic devices and master stations for the electric utility industry. It is now also used in familiar industries like waste water treatment, transportation and the oil and gas industry.	How To Calculate Hex Checksum Where zoning is not needed, it will work perfectly. Where it is desperately needed, it will always break down.

Checksum is used for verifying the integrity of the data. Suppose some file is being copied over a network or over a system and due to some event like network connection loss or sudden reboot of machine the data did not get copied completely.

Now, how would you verify the integrity of data? Well, its through the CRC checksum mechanism the data integrity can be verified. There are various mechanisms through which a CRC checksum can be calculated. For example in one of our articles (IP header check sum) we discussed how to find the checksum of an IP header. In this article, we will focus on the Linux ‘cksum’ command which is used to calculate the check sum of files or the data provided on standard input.

Hex File Crc 16 Calculator Download

What is CRC?

CRC stands for cyclic redundancy check.

Checksum can be calculated by applying cyclic redundancy check (CRC) mechanism over the data that is being communicated. Each block of data that is traveling the communication channel is attached with a CRC code or checksum and when the data block reaches the destination, this check is applied again to generate a checksum value. If the checksum generated at the destination and the checksum value in the data block are same then data is believed to be non-corrupted and can be used further but if the two checksum values are not same then in that case data is said to be corrupted or infected.

The name CRC is because:

• This mechanism is based on the fundamentals of cyclic codes (hence cyclic).
• The code attached with the data as checksum is redundant ie it adds no value to the data being transferred (hence redundancy).
• Its a check (hence check)

The cksum command

Ccitt Crc 16 Calculator

The cksum command is used for computing the cyclic redundancy check (CRC) for each file provided to it as argument. CRC becomes important in situations where data integrity needs to be verified. Using the cksum command, one can compare the checksum of destination file with that of the source file to conclude that whether the data transfer was successful or not.

Besides providing the CRC value, this command also produces the file size and file name in the output. The command exits with status zero in case of success and any other status value indicates failure.

One can get a detailed information on this command by typing the following on the command prompt :

cksum command examples

1. A basic example

On a very basic level, the cksum command can be used to display the checksum for a file.

The first value (big number) in the output above is the checksum for the file, then we have the size of the file and finally the name of the file.

2. Checksum changes with change in content

The test file ‘testfile.txt’ has following contents:

To calculate the checksum of the test file, pass it as argument to the cksum command :

Now, Modify the contents of file :

Again pass the test file as argument to cksum command :

So we see that with change in contents, the checksum changes.

3. Change in content does not always mean increase or decrease in size

Well the above is true fundamentally also and even for chksum too. Lets see what it means :

Check the contents of the test file ‘testfile.txt’ :

Note the checksum :

Now, change the content by not actually adding or deleting something but by replacing one character with other so that size of the file remains same.

So as you can see, I replaced ‘o’ with ‘u’.

Compare the checksum now:

So we see that the checksum changed even if the change was of one character replaced by other.

4. An interrupted copy

Suppose you are copying a zipped folder containing various sub-folders and files from one location to another and due to any reason whatsoever the copy process got interrupted, so how would you check whether everything was copied successfully or not? Well, cksum makes it possible as now we know that in case of the partial copy, the overall checksum of the destination would differ from that of the source folder.

You can simulate this scenario in the following way:

I created Linux.tar.gz and Linux_1.tar.gz from the same ‘Linux’ folder. The difference being that Linux_1.tar.gz was made when ‘Linux’ folder contained an extra text file.

Hex File Checksum Calculator

So the above scenario simulates when Linux_1.tar.gz was being copied but got interrupted when just one text file was left to be copied in the target Linux.tar.gz

Now when I compare the checksum of both these files, I see

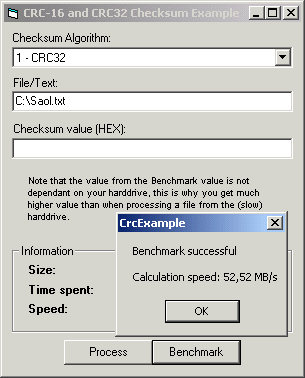
So the above output shows different checksum values suggesting incorrect copy of file.

5. Checksum of standard output

This command provides a feature where-in the user can type just ‘cksum’ or ‘cksum-‘ and write on stdin and then press Ctrl+D couple of times. This way cksum gives the checksum of the data entered at the input.

Hex File Crc 16 Calculator Free

In the example above, we actually calculated the checksum of the string “Lets check the checksum”.